I mean, it’s the easiest disproof to say if 1/0 = 0, then 0*0 must equal 1, which it obviously does not as it would violate the zero property.
Awesome!
You are not wrong, hahaha
Parent should get a conference with teacher and principal. Ask them to show you on a whiteboard how their math works.
Yes, I agree!
It is vital to be engaged with childs education!
bprp is great.
And his ability to effortlessly use a black pen and a red pen in one hand to illustrate changes in equations by step is truly both masterful in it’s delivery and in its performance.
Much respect.
Agree!
Awesome presenter!
edit: added additional info to []
The Zero Ring
It’s just that if you allow it, then all numbers are zero and you get what you deserve
Actually, you CAN divide by zero. [3:51 | Nov 03 2023 | mCoding]
If I have one whole pizza, and I divide it zero times, then wouldn’t I still have one whole pizza? I.e., shouldn’t
1 / 0 = 1?That’s not what division is though. Division, at least when talking about splitting a pizza, has 2 options.
The first is splitting it into X equal parts. If you split a pizza into 0 equal parts, how large is each part?
The other option with pizza would be to say you are splitting into some unknown number of slices of a specific size. if you split a pizza in to slices that are 0 inches wide, how many slices do you get?
Neither method gives any logical result when using 0 with regards to pizza.
I’m not super great at math, and the concept of division by zero has been somewhat confusing for me. It’s also been a bane to my existence as a programmer. To me, in both scenarios, it makes sense to get back the original number, because 0 equal parts and zero inches wide leaves the original pizza untouched. But I also accept that there are much smarter folks out there who know better than I do, so
undefinedorNaNis what it is.Thanks though for explaining it!
The easiest way to explain divide by zero is to think of division as repeated subtraction. For a simple example of 4 / 2 we know that we would have to subtract 2 from 4 twice to reduce it to 0.
When we divide by zero we’re functionally asking how many times can we remove zero from the numerator until it is reduced to zero. We typically state the answer as infinity or NaN because we know that we could do this operation indefinitely without the numerator reducing to 0.
To me, in both scenarios, it makes sense to get back the original number, because 0 equal parts and zero inches wide leaves the original pizza untouched
To illustrate why it’s not the original number, ask yourself this question — “How many times can you slice a pizza such that each slice is 0 inches wide?”
Yes, you’re leaving the pizza untouched with each slice, so you will never stop slicing. Or, you will say zero, because slices that are 0 inches wide are not slices at all. Or you’ll just say it can’t be done.
In this example, when you say “divide it zero times”, what you are really saying is “divide it by 2, zero times”.
So 20=1.
Undefined?
Undefinable.
Dividing by zero? [9:08 | Sep 21 2014 | Eddie Woo]
Time stamp: 2:30 starts to divide 1 by 0
Reddit? This is lemmy. Why are we talking about reddit? I thought the reddit migration was over? Hasn’t enough time passed already for the sensible users to switch from reddit to lemmy?
I think you mean the extremists. The sensible ones stayed.
So since you are here that makes you an extremist?
Anything /0 is considered impossible as an agreement. There’s no actual math involved in that answer. In reality you can divide by 0, but the answer has no natural number.
How many times can you add 0 before you get 1? The answer actually is the drunk(😅) 8 or ‘infinite’, but our minds can’t grasp the very existence of infinite, so we just went with ‘impossible’.
There are ways to circumvent that added concept of some calculators when dividing by 0 anyway and it will show you “Infinite” if it is able to. I remember you could do this in C+ even, but not 100% sure anymore how. I think it was with dividing by an ever decreasing number-variable. When it reaches 0 just before the calculation, C+ didn’t default to an error, but just said ‘Infinite’. But like I said, not 100% sure anymore if that was the actual way.
If your counter against that is that 0 will never become 1 no matter how many you add, then that just proves ‘infinite’ correct. If it ever could, it wouldn’t be infinite…
Sooo, this guy is smart, but also wrong in his calculation here. 😅
Edit: Anyway, voting me down doesn’t change the inconvenient truth above. 😅
the limit of y in 1/x=y as x approaches 0 from negative one is negative infinity. the limit as x approaches 0 from positive one is positive infinity. 1/0 is simultaneously both positive and negative infinity and is paradoxical.
One could argue that negative and possitive infinity, unlike natural numbers, boils down to the same thing, though. Just like 0, infinity technically has no + or -.
Don’t think of infinity as a value. It’s more of a concept to explain numerical behavior. What you described would be like running north at 5 mph south. The limit diverge do it does not exist.
But it is a value. Just one we tend to avoid by claiming it doesn’t exist or is impossible… Our minds just have a hard time imagining it, but that doesn’t mean it doesn’t exist.
Our minds? Infinity isn’t something we don’t understand - we invented the concept of infinity. The mathematics community agreed on its definition, which includes the fact that infinity is not a real number, it literally does not exist. Show me infinity, I’ll give you infinity+1.
You deciding that infinity means something else is not a math problem but a language problem, so if being right about this is that important to you, start a petition or something
So you believe the universe just ends somewhere with nothing behind it?
What’s that got to do with anything? Infinity is just shorthand for “ever-increasing number”.
It is explicitly not a value. The reason you cannot perform arithmetic on infinity is because it has no value. It has cardinality but that is not unique. The set of all integers is infinite as is the set of all real numbers but they have different cardinality as integers are countably infinite whereas real numbers are not countable infinite.
No, it’s not a value. It’s defined as not being a value. No after how much you bend and break maths, infinity will never be a value. Why do you keep telling people wrong things?
If you were to argue this, you’d suddenly break a lot of useful maths. So why would you do so?
I’d only break argumentative math, not actual calculatable math…
Unlike many always say, math has too many agreements and ‘definitions’ and things we added to be universal. On a universal level infinite solves the +/- by the fact it’s infinite…
It breaks calculus, the math that made your phone and has a billion other uses. Directionality of infinities is critical. In calculus, infinity refers only to the magnitude of the resulting vector. Because I suspect you don’t know, integers are a 1-dimensional vector.
Nothing in my phone is either infinite, nor negative.
No but some of the values/specs were calculated by summing an infinite number of infinitely small values. Take a calculus class brother, it’s a cool subject if you’re interested in infinity
Okay, so what? Breaking useful things is bad, no matter what group they belong to. What is positive about no longer being able to use L’Hopital’s rule?
Infinite is not calculable math. If you use infinity in your calculations you will get slapped on the wrists by a math professor.
Google is your friend. I’m gonna leave this here and stop arguing about infinity to people that obviously have no understanding of it.
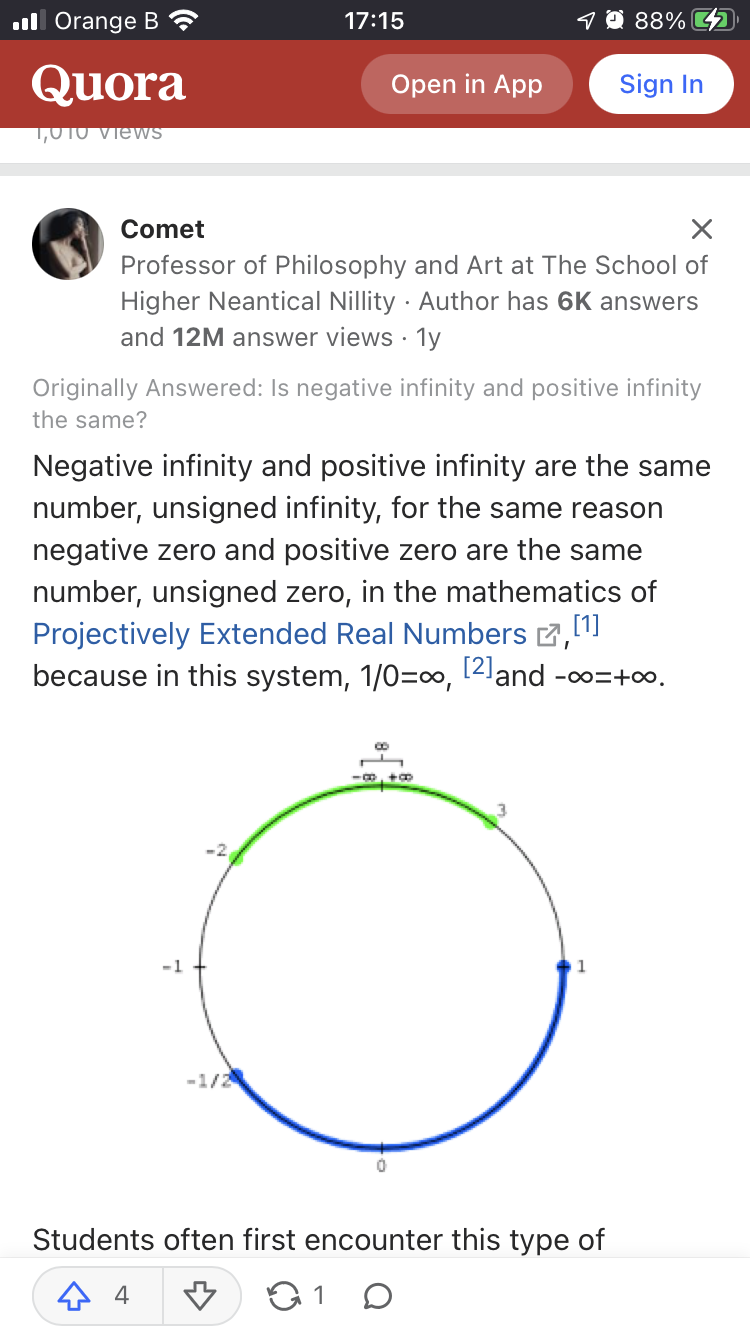 (https://www.quora.com/Is-negative-infinity-equal-to-positive-infinity)
(https://www.quora.com/Is-negative-infinity-equal-to-positive-infinity)Quora has many dubious answers. I wouldn’t use it for any point of argument.
Infinity is not a number. It’s a concept. You’ll find yourself in many paradoxes if you start treating infinity as a number (you can easily prove that 1 = 2 for example).
By your argument, is 1/|x| negative infinity when x is 0? The expression is strictly positive, so it doesn’t make sense to assign it a negative value. But your version of infinity would make it both positive and negative.
Another one: try to plot y = (x^2 - 1) * 1/(x - 1). What happens to y when x approaches 1? If you look at a plot, you’ll see that y actually approaches 2. What would happen if we treat 1/(1-1) as your version of infinity? Should we consider that y could also approach -2, even if it doesn’t make any sense in this context?
We do have a concept of limits in math. That doesn’t mean we ignore it. It is just more correct not to divide by zero as the limits from either side do not converge. Or would you allow -inf as an answer aswell? That is the answer if we approach the limit from the other side.
It is not only convenience but rigor that dictates dividing by 0 to be an erroneus assumption.
It was drilled into my head in school that it’s not a proper limit unless it includes the text “lim A->B”. So using infinity at all, without specifying that you’re taking the limit, would be incorrect. This makes sense as infinity isn’t a real number that you can actually be “equal to”, just a concept you can approach, so you need to specify that by taking the limit, you’re only approaching infinity. I guess the guy you’re replying to needs to hear this more than you though.
Infinite, just like 0, actually has no - or +. So yes and no. For all intents and purposes -inf == inf.
This is completely wrong, please don’t listen to this person.
I suggest you Google “Projectively Extended Real Numbers”.
You mean this one?
The projectively extended real number line is distinct from the affinely extended real number line, in which +∞ and −∞ are distinct.
Now tell me, do we usually work with the projectively extended real numbers?
One positive infinity doesn’t even necessarily equal another positive infinity, as two expressions might not approach infinity at the same rate. Note the word “approach”. That’s the only way you’re allowed to use infinity/-infinity, by approaching it. It’s not a real number, it doesn’t actually exist. Second, in most contexts (calculus) it strictly refers to magnitude (ie, it can have directionality applied to it). Take a calculus class if you want to learn more.
If your counter against that is that 0 will never become 1 no matter how many you add, then that just proves ‘infinite’ correct. If it ever could, it wouldn’t be infinite…
You’re confusing infinity for unreal numbers. Infinity and negative infinity are not real numbers, but not all unreal numbers are infinity or negative infinity.
If you’re strictly adding zeros, then adding infinite zeros nets you zero. If adding zero once didn’t change the result, then adding it infinite times won’t either. If you need to add enough zeros to get to 1, that number doesn’t exist - but that doesn’t mean that it’s infinity, it means that there’s no solution. Infinity is a placeholder for “larger a real number than you can imagine”, but when you multiply that by zero, the magnitude of infinity is a moot point because you have zero infinities.
In calculus if you’re curious, you’re usually not strictly adding zero itself like above but instead adding values that approach zero. In that case, 0*infinity really “a very small number times a really big number”, and that is called an “indeterminate form”. In that case you may try rearranging it to solve
You say it yourself. If you keep adding infinite zeros you will never get 1, hence the ‘divided by 0’ part.
Also, 0 is technically not a number either, it’s the concept of the absence of one. You can’t count 0 things. That doesn’t mean we don’t use it, though. It’s just less hard to imagine and closer to our basic calculations than infinity is.
Zero is a real number, but not a natural number. I’m not going to explain the difference because, dude, this is junior high math
Indeed, and infinite isn’t… It’s like comparing Newton and Einstein on a regular earth scale.
Right, infinity is late high-school, early university math.
Also not really relevant but you know that elementary mechanics approximates the theory of relatively at regular earth scale?
I was always taught it was infinity as opposed to impossible.
Division is defined as the inverse of multiplication. The answer to one divided by zero is the same as asking which number you would multiply by zero in order to get one. No number has that property, not even infinity. So the answer is undefined.
One divided by ‘epsilon’, where epsilon represents a very tiny number, approaches infinity for ever tinier epsilons, so in some maths contexts infinity makes sense. But in general it’s a meaningless question, and so can only have a meaningless answer.
deleted by creator








